Get started with diskers

Kevin Cazelles

02-01-2018

Kernels

There are five kernels currently available, use kernels() to list them all:

kernels()

#>  
#>  Dispersal kernels currently available:
#>  kern_gaussian() --- 2 parameters
#>  kern_exponential() --- 2 parameters
#>  kern_exponential_power() --- 3 parameters
#>  kern_2Dt() --- 3 parameters
#>  kern_lognormal() --- 3 parameters

First parameter is the distance at which the kernel density is evaluated, second is the scale parameter and the third is the shape parameter (for kernels that require 3 parameters):

kern_gaussian(4, 3)
kern_exponential(4, 3)
#
kern_2Dt(4, 3, 2)
kern_exponential_power(4, 3, 2)
kern_lognormal(4, 3, 2)

#>  [1] 0.005977623
#>  [1] 0.004661421
#>  [1] 0.004583662
#>  [1] 0.005977623
#>  [1] 0.001963755

Mean dispersal distance

meanDispDist() return the mean dispersal distance:

meanDispDist('gaussian', 3)
meanDispDist('exponential', 3)
meanDispDist('lognormal', 3, 2)
meanDispDist('k2Dt', 3, 2)
meanDispDist('exponential_power', 3, 2)
meanDispDist('lognormal', 3, 2)

#>  [1] 2.658681
#>  [1] 6
#>  [1] 22.16717
#>  [1] 4.712389
#>  [1] 2.658681
#>  [1] 22.16717

Examples

Below, we exemplify how to plot dispersal isotropic kernels with diskers.

Gaussian kernel

seqx <- seq(0, 10, 0.001)
par(las = 1, bty = 'L')
plot(seqx, kern_gaussian(seqx, .5), type='l', lwd=2, col='#0366d6', xlab='Distance', ylab='Density')

Log_normal kernel

par(las = 1, bty = 'l')
plot(seqx, kern_lognormal(seqx, 3, .2), type='l', lwd=2, col='#0366d6', xlab='Distance', ylab='Density')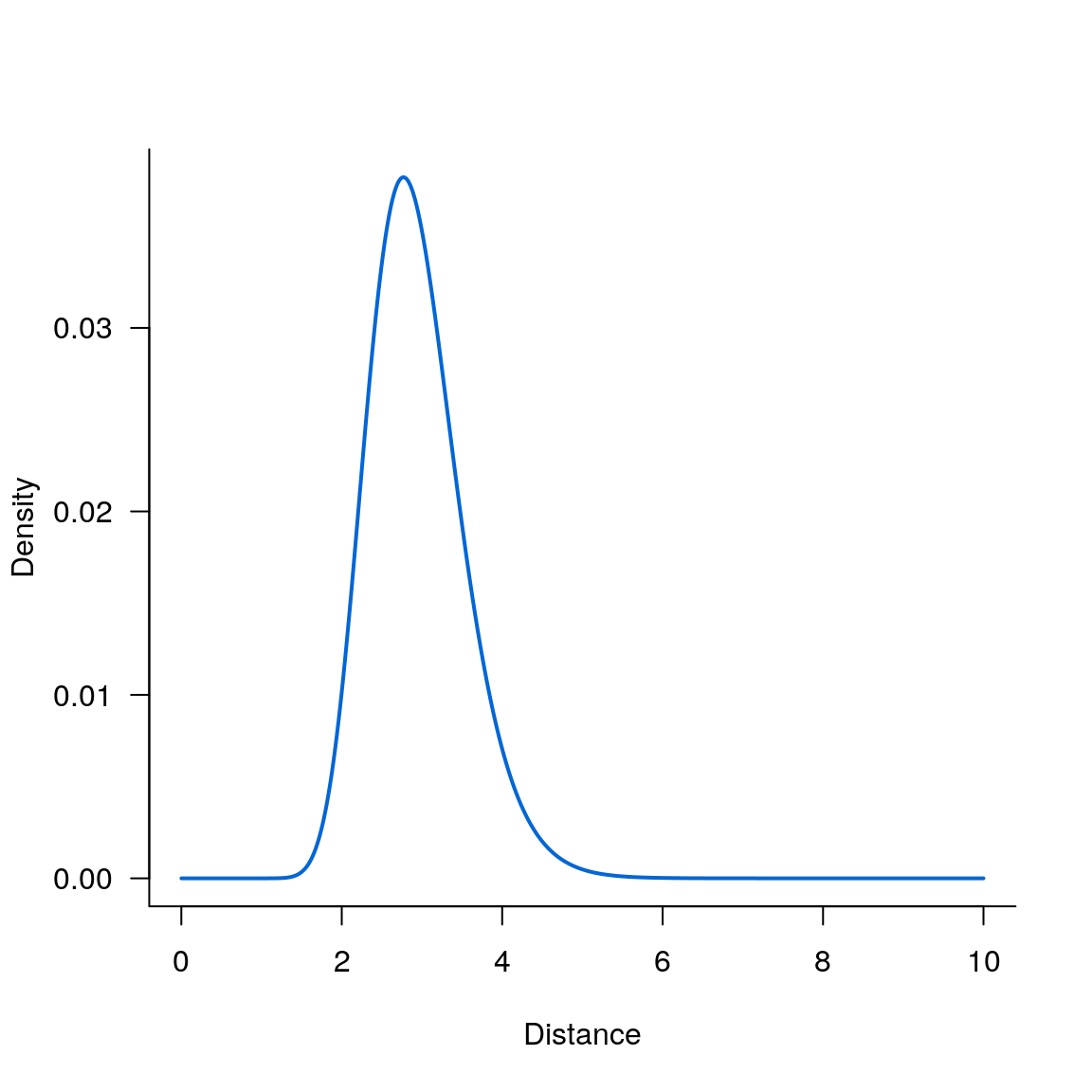

Exponential_power kernel

par(las = 1, bty = 'l')
plot(seqx, kern_exponential_power(seqx,2,3), type='l', lwd=2, col='#0366d6', xlab='Distance', ylab='Density')

References

1. Nathan, R., Klein, E., Robledo-Arnuncio, J. J. & Revilla, E. in Dispersal Ecology and Evolution 186–210 (Oxford University Press, 2012) – doi:10.1093/acprof:oso/9780199608898.003.0015.