Estimation of Food Webs Interactions with Linear Inverse Models

# Estimation of Food Webs Interactions with Linear Inverse Models

.instructors[
  .font180[**Kevin Cazelles, Kevin McCann & Kayla Hale**]
  <br><br>
  .font120[2024-04-24]
]

???
good understanding of what it does and have a broad perspective

---
class: inverse, center, middle

# Introduction

![:custom_hr]()

---
# Linear Inverse Models

### Solve systems of equalities, inequalities and approximations

`$$\mathbf{E} \mathbf{x} = \mathbf{f}$$`

`$$\mathbf{E} \mathbf{x} \approx \mathbf{b}$$`

`$$\mathbf{E} \mathbf{x} \geq \mathbf{g}$$`

]

---
# Linear Inverse Models

### Solve systems of equalities, inequalities and approximations

`$$\mathbf{E} \color{red}{\mathbf{x}} = \mathbf{f}$$`

`$$\mathbf{E} \color{red}{\mathbf{x}} \approx \mathbf{b}$$`

`$$\mathbf{E} \color{red}{\mathbf{x}} \geq \mathbf{g}$$`

]

---
# Linear Inverse Models

### Solve systems of equalities, inequalities and approximations

`$$\mathbf{E} \color{red}{\mathbf{x}} = \mathbf{f}$$`

`$$\mathbf{E} \color{red}{\mathbf{x}} \approx \mathbf{b}$$`

`$$\mathbf{E} \color{red}{\mathbf{x}} \geq \mathbf{g}$$`

]

`$$2\color{red}{x} = 12$$`

</br>

`$$2\color{red}{x} + \color{red}{y} = 12$$`

2 unknown variables, 1 equality

]

---
# Linear Inverse Models

### Solve systems of equalities, inequalities and approximations

`$$\mathbf{E} \color{red}{\mathbf{x}} = \mathbf{f}$$`

`$$\mathbf{E} \color{red}{\mathbf{x}} \approx \mathbf{b}$$`

`$$\mathbf{E} \color{red}{\mathbf{x}} \geq \mathbf{g}$$`

]

`$$2\color{red}{x} = 12$$`

</br>

`$$\color{red}{y} = 12 - 2\color{red}{x}$$`

in other words, a **line**

]

---
# Linear Inverse Models

### Solve systems of equalities, inequalities and approximations

`$$\mathbf{E} \color{red}{\mathbf{x}} = \mathbf{f}$$`

`$$\mathbf{E} \color{red}{\mathbf{x}} \approx \mathbf{b}$$`

`$$\mathbf{E} \color{red}{\mathbf{x}} \geq \mathbf{g}$$`

]

`$$2\color{red}{x} = 12$$`

</br>

`$$2\color{red}{x} + \color{red}{y} = 12$$`

`$$\color{red}{x} > 0;  \color{red}{y} > 0$$`
$$\color{red}{y} < 4 $$
]

all `$(\color{red}{x}, \color{red}{y})$` such as `$\color{red}{y} = 12 - 2\color{red}{x}$` and `$x \in ]4, 6[$` : a **segment**

--
### Large array of problems

- Optimal transportation, clustering, solving Sudoku, etc.
- <svg aria-hidden="true" role="img" viewBox="0 0 640 512" style="height:1em;width:1.25em;vertical-align:-0.125em;margin-left:auto;margin-right:auto;font-size:inherit;fill:currentColor;overflow:visible;position:relative;"><path d="M579.8 267.7c56.5-56.5 56.5-148 0-204.5c-50-50-128.8-56.5-186.3-15.4l-1.6 1.1c-14.4 10.3-17.7 30.3-7.4 44.6s30.3 17.7 44.6 7.4l1.6-1.1c32.1-22.9 76-19.3 103.8 8.6c31.5 31.5 31.5 82.5 0 114L422.3 334.8c-31.5 31.5-82.5 31.5-114 0c-27.9-27.9-31.5-71.8-8.6-103.8l1.1-1.6c10.3-14.4 6.9-34.4-7.4-44.6s-34.4-6.9-44.6 7.4l-1.1 1.6C206.5 251.2 213 330 263 380c56.5 56.5 148 56.5 204.5 0L579.8 267.7zM60.2 244.3c-56.5 56.5-56.5 148 0 204.5c50 50 128.8 56.5 186.3 15.4l1.6-1.1c14.4-10.3 17.7-30.3 7.4-44.6s-30.3-17.7-44.6-7.4l-1.6 1.1c-32.1 22.9-76 19.3-103.8-8.6C74 372 74 321 105.5 289.5L217.7 177.2c31.5-31.5 82.5-31.5 114 0c27.9 27.9 31.5 71.8 8.6 103.9l-1.1 1.6c-10.3 14.4-6.9 34.4 7.4 44.6s34.4 6.9 44.6-7.4l1.1-1.6C433.5 260.8 427 182 377 132c-56.5-56.5-148-56.5-204.5 0L60.2 244.3z"/></svg> https://jump.dev/JuMP.jl/stable/tutorials/linear/diet/

---
# Linear Inverse Models in Food Webs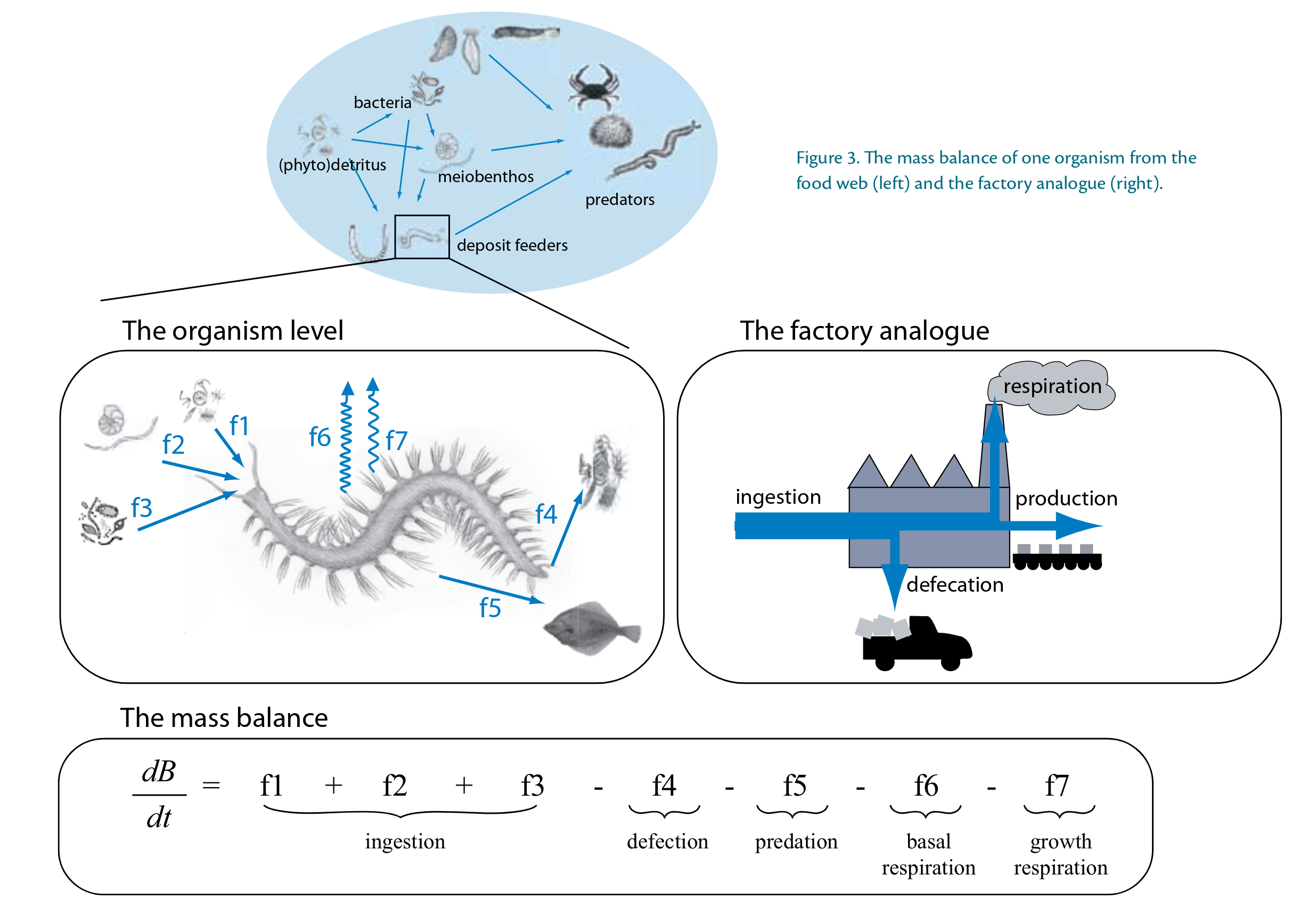

![:scalec 75%](img/biomass_balance.png)

- <svg aria-hidden="true" role="img" viewBox="0 0 448 512" style="height:1em;width:0.88em;vertical-align:-0.125em;margin-left:auto;margin-right:auto;font-size:inherit;fill:currentColor;overflow:visible;position:relative;"><path d="M96 0C43 0 0 43 0 96V416c0 53 43 96 96 96H384h32c17.7 0 32-14.3 32-32s-14.3-32-32-32V384c17.7 0 32-14.3 32-32V32c0-17.7-14.3-32-32-32H384 96zm0 384H352v64H96c-17.7 0-32-14.3-32-32s14.3-32 32-32zm32-240c0-8.8 7.2-16 16-16H336c8.8 0 16 7.2 16 16s-7.2 16-16 16H144c-8.8 0-16-7.2-16-16zm16 48H336c8.8 0 16 7.2 16 16s-7.2 16-16 16H144c-8.8 0-16-7.2-16-16s7.2-16 16-16z"/></svg> Soetaert & Van Oevelen (2009), **Oceanography**.

???
You may know some flows

---
# Linear Inverse Models in Food Webs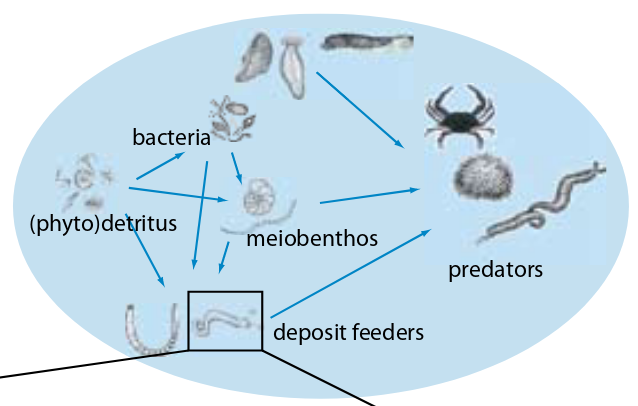

]

- Mass balance (think ECOPATH)

- A set of equalities

- Some knowledge about flows:
  - known parameters: `$f_1 = 2.5$`
  - inequalities: `$f_1 > f_2$`
  - approximations: `$f_1 \approx 2.5$`

---
# Linear Inverse Models in Food Webs

$$\frac{dB_i}{dt} = f_1 + f_2 + f_3 + ... $$

- Using LIM, we obtain a **space**, sets of working flows `$(f_1, f_2, ...)$`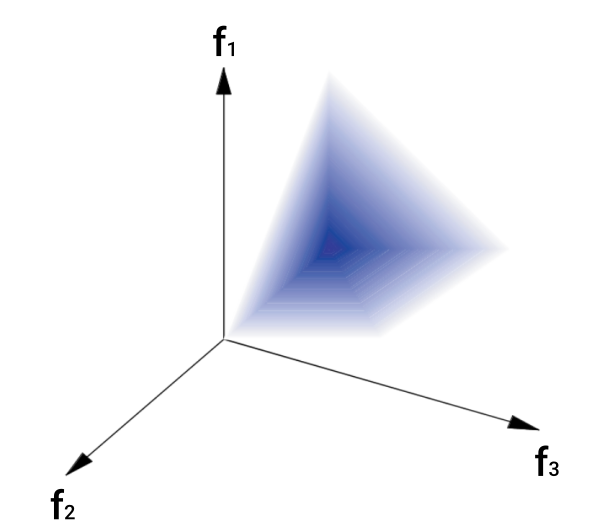

![:scalec 45%](img/space.png)

---
# Linear Inverse Models in Food Webs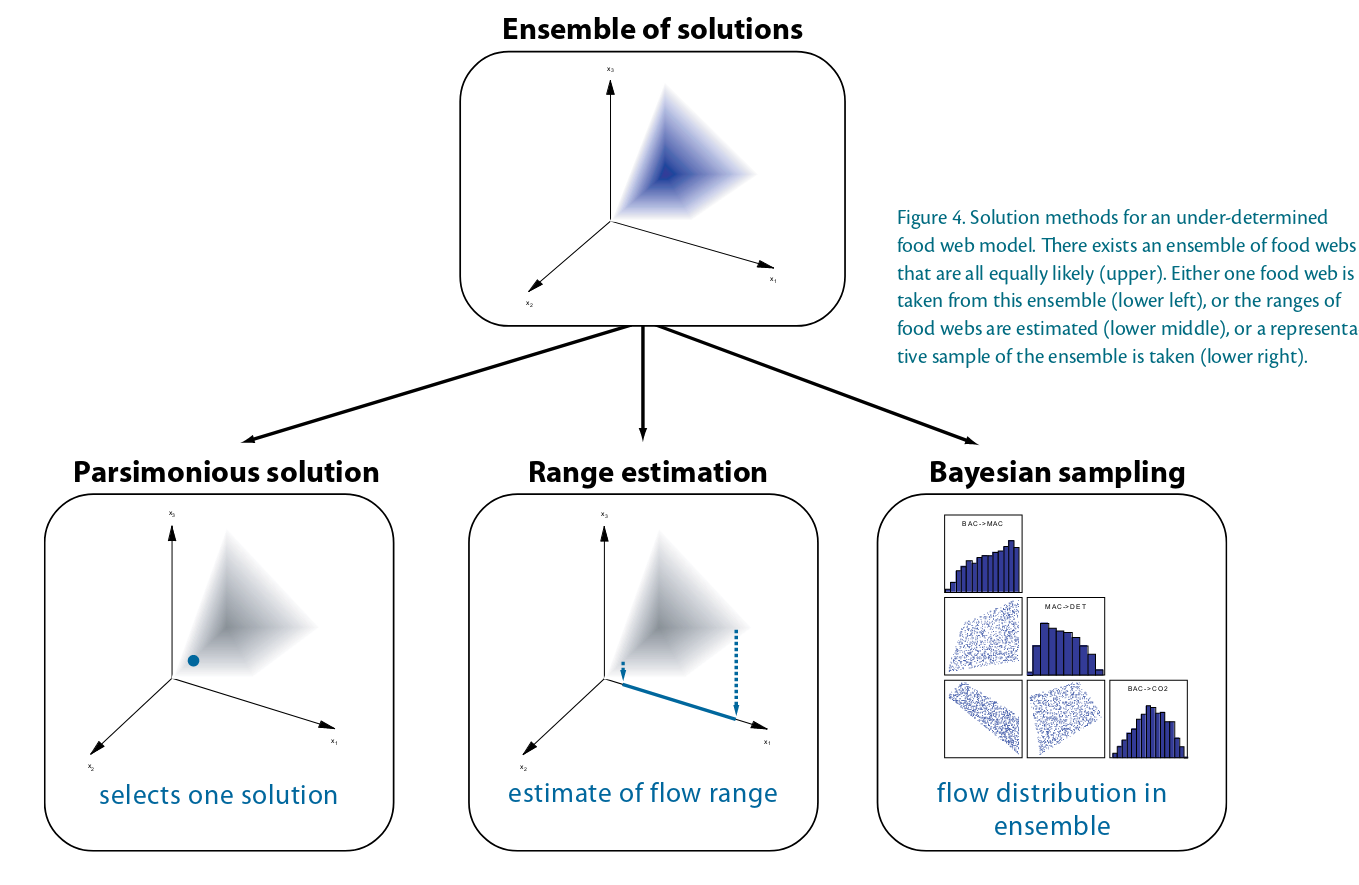

![:scalec 75%](img/results.png)

---

# LIM and food web resilience

![:custom_hr]()

---
# LIM in classical Lotka-Volterra

</br>

`$$\begin{equation}\begin{aligned}
\frac{dPrey}{dt}      &= Prey \left( r_{Prey} + a_{1, 1} Prey - a_{1, 2} Predator \right) \\
\frac{dPredator}{dt}  &= Predator \left( r_{Predator} + a_{2, 1} Prey \right)
\end{aligned}\end{equation}$$`

- Functional response type I

---
# LIM in classical Lotka-Volterra

</br>

`$$\begin{equation}\begin{aligned}
\frac{d\color{red}{Prey}}{dt}      &= \color{red}{Prey} \left( r_{Prey} + a_{1, 1} \color{red}{Prey} - a_{1, 2} \color{red}{Predator} \right) \\
\frac{d\color{red}{Predator}}{dt}  &= \color{red}{Predator} \left( r_{Predator} + a_{2, 1} \color{red}{Prey} \right)
\end{aligned}\end{equation}$$`

- Functional response type I

Classically:

1. interactions are known 
2. we study variations of `$Predator$` and `$Prey$` population (individuals, biomass), the stability of the system

---
# LIM in classical Lotka-Volterra

### Assumptions

- biomass known
- near equilibrium we have:

`$$\begin{equation}\begin{aligned}
\left( r_{Prey} + a_{1, 1} \color{red}{Prey} - a_{1, 2} \color{red}{Predator} \right) &= 0\\
\left( r_{Predator} + a_{2, 1} \color{red}{Prey} \right) &= 0
\end{aligned}\end{equation}$$`

---
# LIM in classical Lotka-Volterra

### Assumptions

- biomass known
- near equilibrium we have:

`$$\begin{equation}\begin{aligned}
\left( r_{Prey} + \color{red}{a_{1, 1}} Prey - \color{red}{a_{1, 2}} Predator \right) &= 0\\ 
\left( r_{Predator} + \color{red}{a_{2, 1}} Prey \right) &= 0
\end{aligned}\end{equation}$$`

### Let's use LIM

- 2 equalities 
- 3 unknown variables: **interaction strengths** that are hard to measure
-  `$Prey$` and `$Predator$` are known: **biomass/population known**
- **Interactions are positive**
- **Interactions are asymmetrical**:
  - conversion efficiency: `$a_{1, 2} > a_{2,1}$`

---
# Sets of interaction strengths

Sets of interactions strengths that lead to the observed biomass

|  `$a_{1,1}$`| `$a_{2,1}$` | `$a_{1,2}$` |
|---------:|-----:|--------:|
| 0.1326175|     1| 1.867382|
| 0.2158816|     1| 1.784118|
| 0.0697550|     1| 1.930245|
| 0.3031896|     1| 1.696810|
| 0.0743744|     1| 1.925626|
| 0.2347560|     1| 1.765244|
| 0.4509523|     1| 1.549048|
| 0.3427189|     1| 1.657281|
| 0.3577168|     1| 1.642283|

---
# Distribution of interaction strengths

![:scalec 75%](img/distrib_2sp.png)

---
# Resilience metric

- We use the Jacobian to determine the **leading eigen value** a proxy for **resilience**

---
# Distribution of interaction strengths

![:scalec 75%](img/distrib_2sp_points.png)

---
# Distribution of interaction strengths

![:scalec 75%](img/distrib_2sp_stab.png)

---
# Distribution of interaction strengths

![:scalec 75%](img/distrib_2sp_stab_res.png)

---
# Most stable system

![:scalec 80%](img/most_stable.png)

???
if stability taken as resilience so...

---
# Least stable system

![:scalec 80%](img/least_stable.png)

---

# Towards Solving Management Challenges With LIM

![:custom_hr]()

???
go over various potential avenues where we can use LIM

---
# A five species example

- 5 species, 10 interactions
- **assumptions**:
  - Lotka-Volterra
  - biomass/population known 
]

.pull-right[
.font50[
|Symbol        | Name                        |
|:------------ |:--------------------------- |
|$$a_{1, 1}$$   | intraspecific competition  |
|$$a_{1, 3}$$   | prey -> predator           |
|$$a_{2, 2}$$   | intraspecific competition  |
|$$a_{2, 4}$$   | prey -> predator           |
|$$a_{3, 1}$$   | predator <- prey           |
|$$a_{3, 5}$$   | predator -> top predator   |
|$$a_{4, 2}$$   | predator <- prey           |
|$$a_{4, 5}$$   | predator -> top predator   |
|$$a_{5, 3}$$   | top predator <- predator   |
|$$a_{5, 4}$$   | top predator <- predator   |
]

]

---
# A five species example

- 5 species, 10 interactions
- **assumptions**:
  - Lotka-Volterra
  - biomass/population known 
]

### constraints

interaction strengths are:

- positive
- asymmetrical `$a_{1,3} > a_{3,1}$`

]

---
# A five species example - resilience

![:scalec 82%](img/distrib_5sp_res.png)

- Potential biostructures and their resilience

---
# Least stable vs. top 25% most stable

![:scalec 90%](img/most_25.png)

---
# Least stable vs. top 10% most stable

![:scalec 90%](img/most_10.png)

---
# Least stable vs. top 1% most stable

![:scalec 90%](img/most_1.png)

---
# Analyzing temporal variations

![:scalec 85%](img/drawing_ts.png)

---
# Structural changes

![:scalec 90%](img/3phases_all.png)

---
# Evolution of the resilience

![:scalec 52%](img/3phases_all_stab.png)

---
# Future Challenges

### A flexible tools to add constraints

- allometric constraints (previous presentation)
- constraints based on time series (variation of biomass)

### Work on real food webs

- This requires **data** (next presentation)
  - food webs topology  (spatially explicit)
  - biomass time series
  - interactions constraints 
 
--

### Expected outcomes

1. Paper: "Towards Solving Management Challenges With LIM"
2. R package: "fwebinfr"
3. Shiny App

---
class: inverse, center, middle

# Interactive tool (Shiny App)

![:custom_hr]()

??? 
very seminal 
very simple 
but useful to know if we want to join force